续探讨Bump-steering在乘用车上的解决和平衡。

乘用车设计考虑的因素比赛车要多得多，要考虑成本、疲劳耐久、维修、还要考虑客户买不买账....总之乘用车上的各种问题，很多都不是彻底解决，而都是在找一个平衡。对于转向系统的Bump-steering 也是一样，我们希望彻底解决Bump-Steering，但从力学角度，我们又希望拉杆恰好处于轮心高度，这样疲劳耐久、上下球销受力要好，所以在乘用车上，很少有彻底全行程内解决Bump-steering...并不是没方案，而是有所不为...

在多体动力学软件大力发展之前，用代数方法解算需要很大的工作量。需要每一个轮心位置解算一系列的方程...所以工程师们更愿意用几何近似的方法来找出近似的位置...

上一节我们了解了，如果将横拉杆布置在A-B或C-D位置，能彻底解决bump-steering, 但乘用车上为了解决力学问题，通常将拉杆布置中间位置，这个时候该如何布置才能更好解决问题。

从悬架瞬心E 出发(关于瞬心可 参考悬架课程第二讲)，连接一条线G-E 。

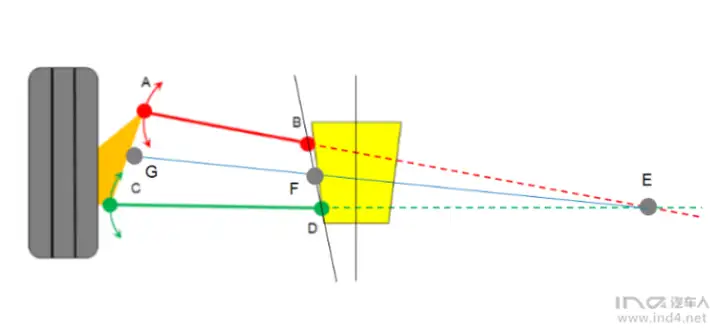
G-E与B-D 的焦点F 就是转向拉杆内点，也就是转向机齿条球销点的位置。

G-F就是转向拉杆...如下图

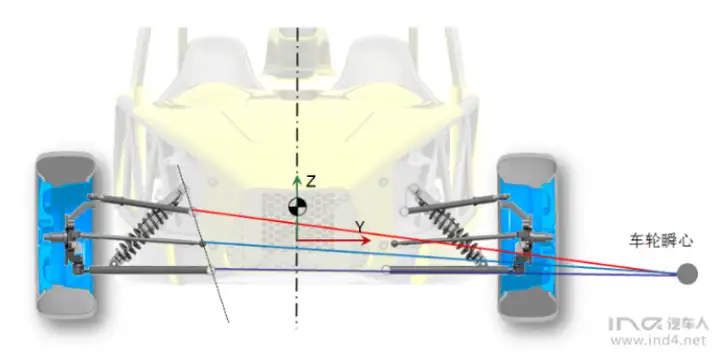
But 很多人估计疑惑了, 上两图，我们只是从车辆Y-Z投影平面进行了点位的探讨。比如F点，我们相当远只定义了Y-Z坐标，如果从车辆Top_View来看，F点X坐标该如何定？ G点更不用说了,虽然在G-E直线上，但在直线上那个位置？X方向呢？是在轮心前方，还是后方？我们下面接续探讨.上面的讨论，其实我们决定的只是G-E 这条线所在的一个平面，F和G 在平面内还有很大的自由度。如下图。

下面继续探讨F、G点的位置探讨，转向系统除过Bump-steering 的特性之外，还有一个响亮的名词叫Ackermann angle（这个理论，本节不做解释），简单来说就是转向时外侧车轮转向角小于内侧转向角，可以保证四轮都纯滚动的转向,为了实现这一转向理论的实现，我们需要合理的布置转向拉杆G点的Y方向值..这么来实现呢！ 如下图

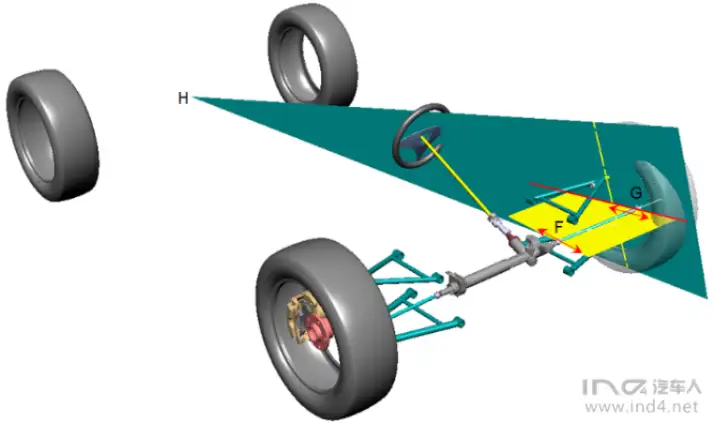
初中几何知识我们都知道，通过直线和直线外一点决定一个平面。在这里我们通过后轴中心点H 和前轮转向主销(关于主销可以参考课程悬架第一讲），创建一个平面（绿色平面）该平面与上述拉杆平面（黄色平面）会产生一个交线（红色），拉杆G点只要落在这条线上对Ackerman 有利。问题又解决了一个。G 点的Y 方向被定义了，现在G点只能在红色交线上移动....

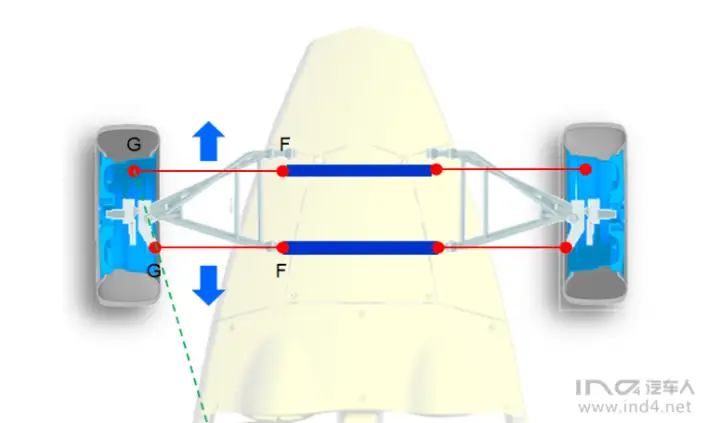
一般的布置上，从Top_View 来看，拉杆内外点处于水平位置（内外点，X 方向坐标相同，但也不绝对），如下图。

外点G的位置可以位于轮心前或者后两个位置，但必须满足落在交线之上.如果你注意观察，可以发现前置拉杆的车辆外点都深入轮辋之内, 而后置拉杆的车辆则外点更靠近车身一些。

从力学角度出发，无论G在轮心前、还是后，我们都希望G点距轮心越远越好。也就是我们所说的转向力臂越大越好，这样可以让拉杆的受力更小，另外从车轮上传递上来的路面反馈也更容易抑制。这个道理很简单，我们开门的时候，离门转轴越远越省力....

具体到布置上，那就是尽量的靠前布置（拉杆前置），或者尽量的靠后布置（拉杆后置）。当然这里最大的障碍便是轮辋的包络（跳动+转向），所以拉杆X方向的布置就只考虑空间关系了。

至此，拉点内，外点的三个方向都有了定义或者限制。我们在做硬点布置的时候就有了依据。